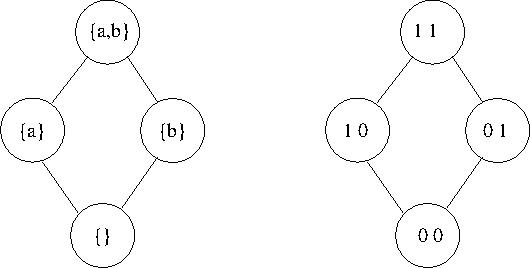
Bilden Sie die Potenzmenge der Menge {a, b, c} und zeichnen Sie ein Diagramm für diese Menge in Analogie zu dem Diagram auf der linken Seite in Abbildung 1, so dass sich Teilmenge, Durchschnitt und Vereinigung im Diagram ablesen lassen. Wie sieht ein entsprechendes Diagramm für eine 1-elementige Menge aus?
Interpretieren Sie das Diagramm auf der rechten Seite in Abbildung 1 so, dass
es sich um komponentenweises ∧ und ∨ handelt. Also zum Beispiel 10 ∧ 01 = 00,
da 1 ∧ 0 = 0 und 0 ∧ 1 = 0.
Zeichnen Sie ein entsprechendes Bild für 111, 110, ...
Können Sie die Beziehung zwischen dem rechten und dem linken Diagram beschreiben? Was bedeutet das für die mengentheoretischen und die logischen Verknüpfungen und für deren Eigenschaften?
Wieviele Elemente hat ein entsprechendes Diagram für eine n-elementige Menge? Wieviele Zeilen hat eine Wahrheitstabelle für n Variablen? Wieviele Gebiete hat ein Venn-Diagram für 1, 2, 3 Mengen?
Wenn Sie noch Zeit haben, versuchen Sie das Diagram für eine 4-elementige Menge zu zeichnen. Was ist das generelle Prinzip für diese Diagramme?
Kann man ein Venn-Diagram für 4 Mengen zeichnen?